Distributed Protocols
In the last lecture we saw
how to program a switch to implement Ethernet learning functionality.
One of the discussion questions asked you to consider what would
happen if the topology contained more than one switch. For the most
part, the Ethernet learning algorithm would work as expected, with one
important caveat: if there is a cycle in the topology, then using the
FLOOD primitive might create a packet storm. In particular,
because Ethernet packets do not have a time-to-live field, there is
nothing to ensure that a packet being forwarded on a loop will
eventually be dropped!
Safe Flooding using Spanning Trees
To ensure that FLOOD works even in the presence of cycles, we need
to somehow prevent it from forwarding packets in a loop. It should be
easy to see that if we construct a tree overlay that connects all
nodes then we can implement a safe version of FLOOD that only
broadcasts packets on ports contained in the tree.
Spanning Tree Protocol
There is a famous distributed protocol for constructing and maintaining a spanning tree due to Radia Perlman. The protocol can be understood in terms of two phases of distributed computation:
-
It elects a node as the root.
-
It computes the shortest paths from every other node back to the root.
Messages and Algorithm
To implement the protocol, each node maintains state with its current best estimates of the root and the distance to the root. In addition, each node periodically sends its best estimates to its neighbors, using a message in the following format:
| Sender | Root | Distance |
|---|---|---|
| A | B | 1 |
Upon receipt of a message from a neighbor, a node updates its state if the information contained in the message is “better” than its current estimates. Assume that node identifiers are totally ordered. The notion of “better” is obtained a follows:
- Smaller root
- Equal root but smaller distance
- Equal root and distance, but smaller node identifier
Properties
Assuming the network topology is connected and eventually stabilizes, one can show that this protocol eventually computes a spanning tree—i.e., there is a unique root and the union of all shortest paths back to the root form a spanning tree.
Distributed Routing
More generally, routers and switches use a variety of distributed protocols to compute network-wide information. For example, suppose we want to compute the shortest paths to each destination in the topology. A classic approach to solving this shortest-path routing problem is to use distance-vector routing. Each node maintains a vector that encodes the estimated distances along the shortest path to every other node in the network. The entries in the distance vector are initialized to ∞, except for the entry for the node itself, which is initialized to 0. Each node periodically sends its distance vector to its neighbor. Upon receipt of a distance vector from a neighbor, a node first adds the distance along the link to that neighbor, then computes the point-wise minimum with its own distance vector, and finally sets its distance vector to the result. In addition, to be able to route traffic, the node records the neighbor that is on the next hop toward each destination.
Example
To illustrate, consider the following topology,
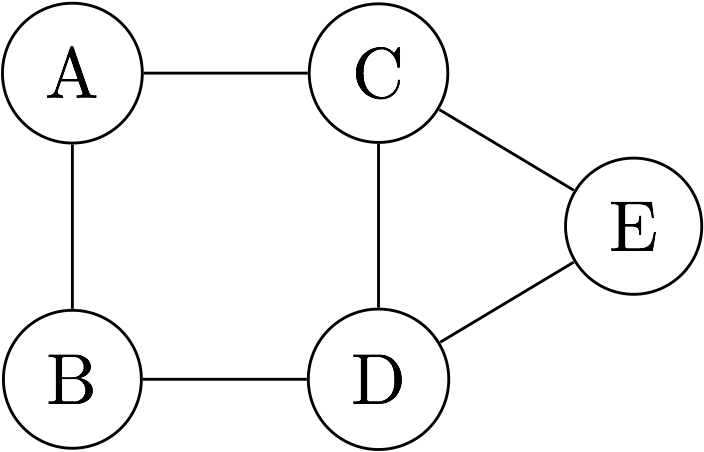
and consider the execution of the protocol at router A. For simplicity, assume that the distance between neighboring nodes is 1.
The initial state at router A is as follows:
| Node | A | B | C | D | E |
|---|---|---|---|---|---|
| Distance | 0 | ∞ | ∞ | ∞ | ∞ |
| Next Hop | ? | ? | ? | ? |
Upon receiving the following distance vector from router B,
| Node | A | B | C | D | E |
|---|---|---|---|---|---|
| Distance | ∞ | 0 | ∞ | 1 | ∞ |
Router A updates its state to the following:
| Node | A | B | C | D | E |
|---|---|---|---|---|---|
| Distance | 0 | 1 | ∞ | 2 | ∞ |
| Next Hop | B | ? | B | ? |
Similarly, upon receiving the folowing distance vector from router C,
| Node | A | B | C | D | E |
|---|---|---|---|---|---|
| Distance | ∞ | ∞ | 0 | 1 | 1 |
A updates its state to the following:
| Node | A | B | C | D | E |
|---|---|---|---|---|---|
| Distance | 0 | 1 | 1 | 2 | 2 |
| Next Hop | B | C | B | C |
Note that there are two equal-cost paths to router D, one via router B and another via router C. Here we break the tie by keeping the existing path via router B, which has a “smaller” identifier. When the protocol quiesces, every node be able to forward packets along the shortest path to its destination.
Limitations
Unfortunately, distance vector protocols suffer from a number of well-known limitations. One issue is that information about changes to the network can propagate through the network slowly. For example, if a new link becomes available that changes some shortest paths, nodes that are far away from the link will only update their state after all of the nodes on the path exchange information with the new update. Moreover, depending on how these exchanges are staged, stale information may propagate for several “rounds” of communication.
A more serious problem is that the protocol does not guarantee that all of the intermediate paths encountered will be free of forwarding loops. To illustrate, consider the following topology:

Suppose the protocol quiesces in a state where router A’s distance vector is as follows:
| Node | A | B | C |
|---|---|---|---|
| Distance | 0 | 1 | 2 |
| Next Hop | B | B |
Now consider what happens if router C goes down. Even if router B realizes that its neighbor no longer exists, it may receive a message from router A stating that it can reach router C in two hops. Due to the simple messages exchanged in a distance-vector protocol, router B will have no way to realize that router A’s path to router C goes through B itself so it will simply update its distance vector with the information that it can reach router C in three hops, creating a forwarding loop! Worse, router B will then send a new message to A stating that it can reach router C in three hops, so router A will update its own distance vector with the information that it can reach router C in four hops, and so on. This phenomenon is known as the count-to-infinity problem.
There are several effective ways to mitigate this problem:
-
Path-Vector Protocols: messages carry information about the complete forwarding path rather than just distances
-
Split-Horizon Advertisements: information about a destination is never propagated back to the neighbor that provided it.
-
Poisoning: special messages indicating that a node has become unreachable.
-
Hold-Down: delaying updates involving nodes that have recently become unreachable for a fixed period of time.
But the details of each these solutions are subtle, and they significantly complicate the overall protocol.
Discussion
-
Can you prove the properties claimed for the spanning tree protocol and distance vector routing?
-
How long do these protocols take to converge? Can this be improved?