NetKAT Compilation

Over the last few lectures, we have explored a number of theoretical aspects of the NetKAT language, including an equational deductive system and automata-theoretic semantics. But to be able to use the language in practice, we need to be able to compile programs into forwarding rules that can be installed on OpenFlow switches.

Overview

A key challenges that arises when compiling a NetKAT program is translating programs into equivalent forwarding rules in an efficient manner. In this lecture we will develop an algorithm for doing this, in the case where the NetKAT program is local – i.e., it only specifies local packet-processing on individual switches. Formally, a local program can be characterized syntactically as one that does not contain any modifications to the switch field or any occurrences of dup.

Naive Compilation

A straightforward way to compile local programs is to define a translation that maps each atomic program into a forwarding table, and then “lift” each of the NetKAT operators to equivalent operators on forwarding tables. For example, to compile a test f=n we would produce the following table:

Match	Action
f = n	Output(Inport)
*	Drop

Similarly, to compile a modification f := n we would produce the following table:

Match	Action
*	ModifyField(f,n)

To compile a union p1 + p2, we need to produce a table with three distinct kinds of rules:

1. For packets in the domain of p1 and p2
2. For packets in the domain of p1 but not in the domain of p2
3. For packets not in the domain of p1 but in the domain of p2

We first recursively translate p1 and p2 tables t1 and t2. To produce the rules for 1, we compute an all-pairs intersection of the rules in t1 and t2, concatenating their matches and actions. To produce the rules for 2 and 3 we simply append the rules in tables t1 and t3 in either order. (Some readers may have observed that concatenating actions does not correctly implement the semantics of union in all situations – e.g., consider a program that modifies two distinct fields and outputs the resulting packets; these situations can be handled by a more complex translation that matches on the possible original values of one of the fields being modified, but this approach leads to much larger forwarding tables.)

Sequential composition p1; p2 can be handled via a similar translation.

Unfortunately this approach has two limitations:

1. It uses a quadratic algorithm to combine forwarding tables, which leads to poor performance on large programs.

2. It is unclear how to compile Kleene star – a naive fixpoint computation may not terminate as there are infinitely many equivalent forwarding tables for each function on packets.

Forwarding Decision Diagrams

To address these problems, we switch perspective and adopt a different data structure: Forwarding Decision Diagrams (FDDs). The rationale for using FDDs stems from the observation that a forwarding table is essentially a Boolean packet classifier, with associated actions. In many other domains, Binary Decision Diagrams (BDDs) have been successfully used to represent and manipulate Boolean functions, so it seems likely they would also be useful for representing forwaring tables.

To a first approximation, an FDD can be thought of as a binary tree where every node is labeled with a test and the leaves are annotated with a set of actions – i.e., a list of modifications. By convention we will let the first child represents the “true” branch and the second child represents the “false” branch. Formally, we can define the syntax and semantics of FDDs as follows:

-- Actions
a ::= [ f1 := n1; ...; fk := nk ]

[[ a ]] : Packet -> Packet

[[ f1 := n1; ...; fk := nk ]] pk =
  pk[fi <- ni | i in { 1 .. k } ]
    
-- Forwarding Decision Diagrams
d ::= { a1 + ... + ak }
    | f = n ? d1 : d2

[[ d ]] : Packet -> Packet Set
    
[[ { a1 + ... + ak } ]] pk =
  { [[ ai ]] pk | i in { 1 .. k } }
    
[[ f = n ? d1 : d2 ]] pk =
  { [[ d1 ]] pk   if pk.f = n
  { [[ d2 ]] pk   otherwise    

Note that { } denotes the function that drops all packets while { [ ] } denotes the identity function that maps pk to { pk }.

We can impose extra conditions to simplify diagrams:

• Use hash consing to ensure that common sub-diagrams are only represented once.

• Eliminate redundant tests – i.e., forbid tests involving f in true branch of f = n ? d1 : d2 and replace f = n ? d1 : d2 with d1 when d1 = d2.

• Impose an total order on tests and require that the sequence of tests on all paths through the diagram respect that order.

These conditions are based on analogous conditions for reduced, ordered BDDs. However, reduced, ordered FDDs are not canonical, unlike BDDs.

Compiling with FDDs

Next, let us define the NetKAT operations on FDDs. To shorten the definitions, we omit symmetric cases.

Union

(a11 + ... + a1k) + (a21 + ... + a2l) =
    (a11 + ... + a1k + a21 + ... a2l)
    
(f = n ? d11 : d12) + (a21 + ... + a2l) =
    f = n ? d11 + (a21 + ... + a2l) : d21 + (a21 + ... + a2l)

(f1 = n1 ? d11 : d12) + (f2 = n2 ? d21 : d22) =
    { f1 = n1 ? d11 + d21 : d12 + d22 if f1 = f2 and n1 = n2   
    { f1 = n1 ? d11 + d22 : (f2 = n2 ? d21 : d22) if f1 = f2 and n1 < n2
    { f1 = n1 ? d11 + (f2 = n2 : d21 : d22) : d12 + (f2 = n2 : d21 : d22) if f1 < f2

In this definition, we are careful to respect the ordering on tests, which we assume is defined lexicographically in terms of an ordering on fields and patterns. Readers familiar with BDDs might observe that this is the standard “apply” algorithm, using the “+” operation to combine leaves.

Seqeunce

We first define an auxiliary “restriction” operation d|_a where a is a positive or negative test.

(a11 + ... + a1k)|_{f=n} =
    (f = n ? (a11 + ... + a1k) : ())    

(f1 = n1 ? d11 : d12)|_{f=n} =
    { f = n ? d11 : () if f = f1 and n = n1
    { (d12)|_{f=n} if f = f1 and n != n1
    { f = n ? (f1 = n1 ? d11 : d12) : ()) if f < f1
    { f1 = n1 ? (d11)|_{f=n} : (d12)|_{f=n} otherwise

Next we define a composition operation for the special case where the left hand term is an action:

a1 ; (a21 + ... + a2l) =
    (a1; a21 + ... a1; a2l)

a1; (f2 = n2 ? d21 : d22) =
    { a1; d21 if f := n in a1
    { a1; d21 if f := n1 in a1 and n != n1
    { (f = n ? a1; d21 : a1: d22) otherwise

Finally, we can define sequential composition on diagrams.

(a11 + ... + a1k); d2 = (a11; d2 + ... ; a1k; d2)
(f = n ? d11 : d12) ; d2 = (d11 ; d2)|_{f = n} + (d21 ; d2)|_{f != n}

Negation

!{} =
    []
    
!{ a1; ...; ak } =
    {} where k >= 1

!(f = n ? d1 : d2) =
    (f = n ? !d1 : !d2)            

The correctness of this definition depends on the fact that negation is only ever applied to predicates.

Iteration

d* = fix (fun di -> { [] } + d; di)

Unlike tables, there are only finitely many reduced, ordered FDDs, so the fixpoint is guaranteed to terminate.

Translation

Using these operations, the compilation from NetKAT to diagrams is straightforward:

(| 0 |) = { }
(| 1 |) = { [ ] }
(| f = n |) = f = n ? { [] } : { }    
(| f := n |) = { [ f := n ] }
(| !p |) = ! (| p |)
(| p* |) = (| p |)*
(| p1 + p2 |) = (| p1 |) + (| p2 |)
(| p1 ; p2 |) = (| p1 |); (| p2 |)                     

From Diagrams to Forwarding Tables

To generate a forwarding table, we simply traverse paths in the FDD, starting with the all-true path, taking the conjunction of each tests on the path and using the actions at the leaves, as captured by the following pseudo-code:

let forwarding_table_of_fdd d =
  let rec loop pred d =
    match d with
    | { a1, ..., ak } -> (pred, {a1, ..., ak })
    | f = n ? d1 : d2 -> loop d1 (f = n :: pred) @ loop d2 pred in
  loop [] d

Global Compilation

So far, we’ve seen how to compile local NetKAT programs to forwarding tables. Of course, that’s only half the story – we also need a translation that maps global programs to local programs. There are two main challenges related to global compilation (i) in general, we will need to add state to the packet to keep track of the execution of the global program, but (ii) to implement NetKAT’s set-based semantics, we need to be careful not to introduce state that would generate extra packets.

Approach

The approach we will follow is to use the representation of NetKAT programs as automata. Recall that a NetKAT automataon M is a 4-tuple (Q, q0, d, e) where

• Q is a finite state of states
• q0 in Q0 is the initial state
• d in State * Packet -> (State * Packet) Set is the transition function
• e in State * Packet -> Packet Set is the observation function

We can construct automata using derivatives.

The global copmilation algorithm goes as follows.

1. We convert the input program p to an automaton M and determinize.

2. We internalize the state by adding a new field pc and guarding each of the transitions and observations in state q by the test for pc=q.

3. We guard each of the links to test for the locations at each end-point. This transformation makes it possible to replace a link with the entire topology without changing the semantics of the program.

4. We modify the program implement transitions for the pc by exploiting the following observations. First, by construction the automaton has a bipartite structure, alternating between switch states and topology states. Second, every link has just two end-points. Hence, the successor state of a switch state after going over a particular link is distinct. We can use this insight to “fast-forward” across the hop, and update the pc to the next switch state.

5. Finally, we collect up the programs for all of the switch states, and take the union of their transition and observation functions. The result is a local program.

Example

To see this compiler in action, suppose that the topology is a “barbell” with switches numbered 1 and 3, with external ports 1 and 2 and an internal ports 3. Now suppose we wish to forward on the upper and lower paths. This behavior can be implemented in NetKAT as follows

filter (switch=1);
 (filter (port=1); port:=3; 1@3=>3@3; port:=1 +
  filter (port=2); port:=3; 1@3=>3@3; port:=2 )    

Here we use the syntax supported by the NetKAT implementation, which requires writing filter before a predicate.

This program can be converted into the following automaton:

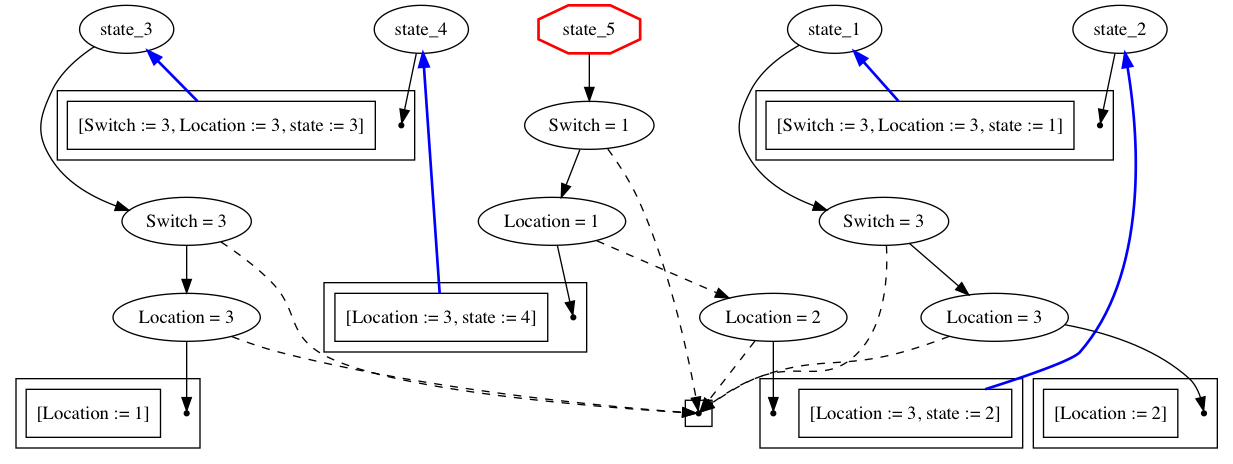
The start state, state_5 is labeled with a “stop sign” symbol. In each state, we have an FDD that represents the packet-processing up to the next link and blue edges to indicate the transitions to successor states. By inspecting the FDD for the start state, we can see that we either transition to state_4 if the packet is located at port 1, or to state_2 if it is located at port 2. In either case, the packet is forwarded to port 3 on switch 3.

Using the vlan field to encode the pc, we obtain the following forwarding tables:

+----------------------------------------+
| Switch 1 | Pattern | Action            |
|----------------------------------------|
| InPort = 1         | SetField(vlan, 3) |
|                    | Output(3)         |
|----------------------------------------|
| InPort = 2         | SetField(vlan, 1) |
|                    | Output(3)         |
|----------------------------------------|
|                    |                   |
+----------------------------------------+

+--------------------------------+
| Switch 3 | Pattern | Action    |
|--------------------------------|
| InPort = 3         | Output(2) |
| Vlan = 1           |           |
|--------------------------------|
| InPort = 3         | Output(1) |
| Vlan = 3           |           |
|--------------------------------|
|                    |           |
+--------------------------------+    

Determinization

To understand the importance of determinization, consider what would happen if we naively tried to compile p + p, using the pc to keep track of the two sub-terms in the program. According to the NetKAT semantics, p + p is equivalent to p so we should not duplicate packets. However, it can be challenging to decide when it is necessary to create a copy of the input packet – the copy may eventually become identical to the original packet at some other switch.

The solution turns out to be simple: determinize the automaton. To illustrate the difference, consider the following program in a two-switch topology organized in a linear chain:

(filter (switch=1 and port = 1);
    port := 2; 1@2 => 2@2; port := 1) +
(filter (switch=1 and port = 1 and ip4Dst = 10.0.0.1);
    port := 2; 1@2 => 2@2; port := 1)    

The packets produced by the second clause are a subset of the first. Yet the automaton generated using derivatives is as follows:

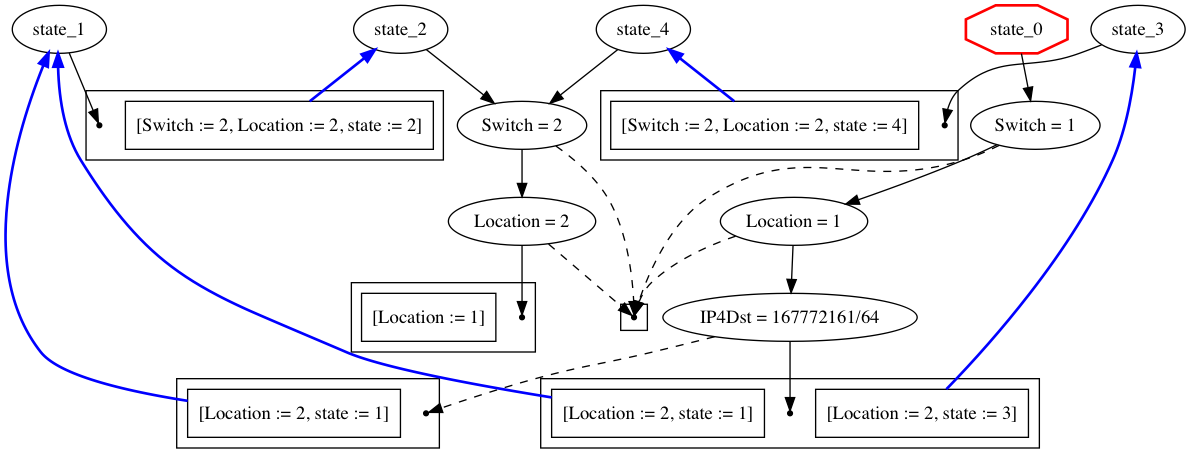
Note that naively interpreting this automaton would produce extra outputs due to the actions in the start state which copies the input packet.

However, if we determinize, using a close variant of the subset construction, then we get the following automaton:

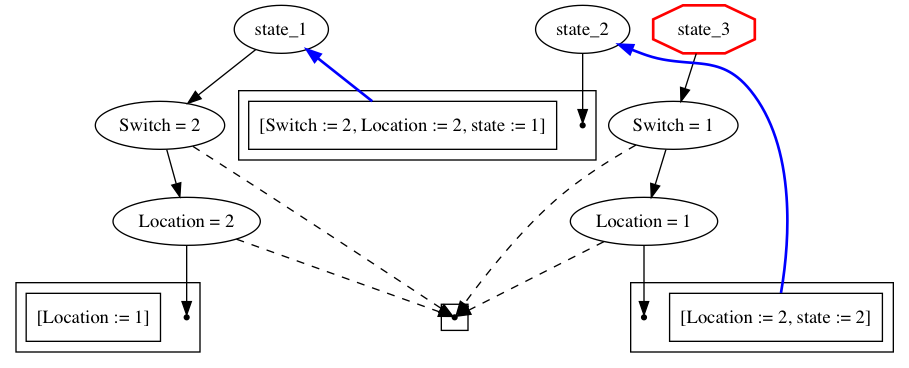
which compiles to the following flow table:

+----------------------------------------+
| Switch 1 | Pattern | Action            |
|----------------------------------------|
| InPort = 1         | SetField(vlan, 1) |
|                    | Output(2)         |
|----------------------------------------|
|                    |                   |
+----------------------------------------+

+--------------------------------+
| Switch 2 | Pattern | Action    |
|--------------------------------|
| InPort = 2         | Output(1) |
| Vlan = 1           |           |
|--------------------------------|
|                    |           |
+--------------------------------+        

Reading

This lecture is based on the following paper:

• A Fast Compiler for NetKAT